R Programming 2024 Regular Solved Question Paper

RP Regular 2024 (NEP) Solved Question Paper Questions with Answers

R Programming 2 Marks (IMP)

Section - A

Answer any TEN questions. Each question carries 2 marks. (10*2=20)

1. List the basic datatypes in R.

Numeric
Integer
Character
Logical
Complex
Raw

2. Define list in R. Write an example to create a list.

A list in R is a versatile data structure that can store collections of objects of different types. Unlike vectors that require all elements to be of the same type, a list can contain elements of varying types, such as numbers, strings, vectors, and even other lists.

Example:

# Create a list
my_list <- list(
  name = "Alice",
  age = 30,
  city = "New York",
  hobbies = c("reading", "coding", "hiking")
)

# Print the list
print(my_list)

3. What do you mean by special values ? Give example.

In R programming, “special values” refer to specific values that have unique meanings or usages and may deviate from standard data types. These values are often used to represent missing, undefined, or infinite values, and they play important roles in data analysis and statistical computations.

#Example of Inf
y <- 1/0
print(y) # Outputs: Inf

4. Mention the different assignment operators in R with examples.

<-: Left assignment
->: Right assignment
=: Assignment (similar to <-)
<<-: Global assignment
assign(): Assign using variable name as a string.

Two Examples of Assignment Operator in R:

<-: Left assignment

Ex: x <- 10
# x now holds the value 10

->: Right assignment

20 -> y 
# y now holds the value 20

5. Differentiate between cat ( ) and Print ( ) functions.

print()	cat()
Prints objects in a human-readable format	Concatenates and outputs as a single string
Returns the object	Returns NULL
Displays quotes around character strings	No quotes around character strings
Automatically adds line breaks for multi-line output	No line breaks unless explicitly specified (e.g., \n)
Suitable for data frames, lists, and vectors	Better for formatted text or simple output
Uses space or newline for multi-line data	No default separator; use sep argument for custom separators
Inspecting or debugging objects	Producing formatted output or reports

6. Write the syntax of “while” and “repeat” statements in R.

Syntax of While Statement.

while (condition) {
# Code to be executed
}

Syntax of Repeat Statement.

repeat {
# Code to be executed
if (condition) {
break
}
}

7. Write the purpose of prod ( ) and round ( ) functions. Give example for each.

1. prod() Function

The prod() function calculates the product of all elements in a numeric vector. It’s useful for multiplying a series of numbers together.

Example:

numbers <- c(2, 3, 4)
result <- prod(numbers)
print(result)
# Output: 24 (since 2 * 3 * 4 = 24)

2. round Function

The round() function rounds numbers to a specified number of decimal places. By default, it rounds to the nearest whole number, but you can specify the number of decimal places.

Example:

number <- 3.14159
rounded_number <- round(number, digits = 2)
print(rounded_number)
# Output: 3.14 (rounded to 2 decimal places)

8. List any four functions on set operations.

union(x, y): Combines all unique elements from both sets.
intersect(x, y): Finds common elements between sets.
setdiff(x, y): Elements in x but not in y.
setequal(x, y): Checks if two sets are identical

9. Define normal distribution.

Normal Distribution is a probability function used in statistics that tells about how the data values are distributed.

10. What is ANOVA? Write the notations for Null and alternative hypothesis.

ANOVA (Analysis of Variance) is a statistical method used to determine whether there are any statistically significant differences between the means of three or more independent groups.

Notations:

1. Null Hypothesis ( $H_0$ )

The Null hypothesis represents the default assumption or the hypothesis that there is no effect, no difference, or no relationship between variables. It is often the hypothesis you are trying to disprove.

Notation in R:

H0 <- "Null Hypothesis"

2. Alternative Hypothesis ( $H_a$ or $H_1$ )

The Alternative hypothesis represents the hypothesis that there is an effect, a difference, or a relationship between variables. It is what you are trying to prove or provide evidence for.

Notation in R:

Ha <- "Alternative Hypothesis"

11. Write the purpose and syntax of Im ( ) function in R.

The Im() function is used to extract the imaginary part from a complex number or complex vector.

Syntax:

Im(x)

12. What are regions and margins in a R plot?

Regions: These are the main areas of the plot where the data is displayed. For example, in a scatter plot or line graph, the region is the part where the axes and data points are plotted.
Margins: These are the spaces around the plot region, typically used for axis labels, titles, or annotations. In R, the par(mar = c(bottom, left, top, right)) function is used to adjust the size of the margins.

Section - B

Answer any FOUR from the following questions. Each question carries 5 marks. (4*5=20)

13. Define vector in R. Explain the different ways of creating a vector.

vector is one of the most fundamental data structures used to store a sequence of data elements of the same type. Vectors can hold various types of data, including numeric, character, and logical values

Example:

# Vector of strings
fruits <- c("banana", "apple", "orange")

# Print fruits
fruits

Key Characteristics of Vectors in R:

Homogeneous: All elements in a vector must be of the same type.
One-dimensional: Vectors have no rows or columns (unlike matrices or data frames).
Indexed: Elements of a vector can be accessed by their position (starting from index 1).

Different ways of creating a vector:

1. Using vector() Function

The vector() function creates an empty vector of a specified type and length.

Syntax:

vector(mode = "type", length = n)

Example:

# Create an empty numeric vector of length 5
empty_vec <- vector(mode = "numeric", length = 5)
print(empty_vec)

2. Using as.vector() Function

The as.vector() function converts other objects, like matrices or lists, into a vector.

Syntax:

as.vector(object, mode = "type")

Example:

# Convert a matrix into a vector
mat <- matrix(1:6, nrow = 2)
vec_from_mat <- as.vector(mat)
print(vec_from_mat)

3. Using seq() Function (Generate a Sequence)

The seq() function is used to create a sequence with more control, such as specifying step size.

Syntax:

seq(from = start, to = end, by = step)

Example:

# Sequence from 1 to 10 with step size 2
seq_vec <- seq(from = 1, to = 10, by = 2)
print(seq_vec)

4. Using rep() Function (Replication)

The rep() function repeats elements in a specific way to generate a vector.

Syntax:

rep(x, times = n)       # Repeat x 'n' times
rep(x, each = n)        # Repeat each element of x 'n' times

Example:

# Repeat the vector 3 times
rep_vec1 <- rep(c(1, 2, 3), times = 3)
print(rep_vec1)

# Repeat each element 2 times
rep_vec2 <- rep(c(1, 2, 3), each = 2)
print(rep_vec2)

14. What is recursion? Write an R program to find the factorial of a number using recursion.

Recursion is a programming technique in which, a function calls itself repeatedly for some input

R Program To find Factorial of given number using recursion. 

# Function to find factorial using recursion 
factorial_recursion <- function(n) 
{ 
 if (n == 0 || n == 1) 
 { 
  return(1) # Base case: factorial of 0 and 1 is 1 
 } 
 else 
 { 
  return(n * factorial_recursion(n - 1)) # Recursive call 
 } 
} 


# Input number for factorial calculation 
num <- as.integer(readline("Enter A integer number : ")) 

# Call the factorial function 
result <- factorial_recursion(num) 

# Print the result 
cat(paste("Factorial of", num, "is", result)) 


Output : 

Enter A integer number : 3 
Factorial of 3 is 6

15. What is a file? Explain any four file handling functions in R.

A file refers to a collection of data that is stored on a disk. Files can hold various types of information, such as text, numbers, or binary data, and can be read from or written to using R functions. File handling in R is essential for data input and output operations, allowing users to load data for analysis or save results.

Function	Purpose	Example
`file()`	Creates a connection to a file.	`file("example.txt", open = "r")`
`read.table()`	Reads structured data into a data frame.	`read.table("data.txt", header = T)`
`write.csv()`	Writes a data frame to a CSV file.	`write.csv(iris, "iris.csv")`
`file.exists()`	Checks whether a file or directory exists.	`file.exists("example.txt")`

File Handling Functions in R

1. file() Function

The file() function creates a connection to a file for reading, writing, or appending.

Syntax:

file(description, open = "r", blocking = TRUE)

Example:

# Open a file for writing
file_conn <- file("example.txt", open = "w")

# Write data to the file
writeLines("This is an example file.", file_conn)

# Close the file connection
close(file_conn)

2. read.table() Function

The read.table() function is used to read data from a file into a data frame. It is suitable for reading text files or CSV files where the data is structured in rows and columns.

Syntax:

read.table(file, header = FALSE, sep = "", ...)

Example:

# Create and read a data file
write.table(mtcars, file = "cars_data.txt", sep = "\t", row.names = FALSE)

# Read the file into R
data <- read.table("cars_data.txt", header = TRUE, sep = "\t")
print(data)

3. write.csv() Function

The write.csv() function is used to write data frames or matrices to a CSV file (comma-separated values).

Syntax:

write.csv(x, file, row.names = TRUE)

Example:

# Write the iris dataset to a CSV file
write.csv(iris, file = "iris_data.csv", row.names = FALSE)

# Check the file in the working directory
print("CSV file written successfully!")

4. file.exists() Function

The file.exists() function checks whether a specified file or directory exists.

Syntax:

file.exists(file)

Example:

# Check if the file "example.txt" exists
if (file.exists("example.txt")) {
    print("The file exists!")
} else {
    print("The file does not exist.")
}

16. Compute the mean and median for the following observations: (9,5,2,3,4,6,7) Mention the R functions for the same.

Given Observations:

Data: (9, 5, 2, 3, 4, 6, 7)

R Functions

Mean Calculation: The mean is calculated by taking the sum of the observations and dividing it by the number of observations.
R Function: mean()
```
observations <- c(9, 5, 2, 3, 4, 6, 7)
mean_value <- mean(observations)
```
Median Calculation: The median is the middle value when the observations are sorted. If there is an odd number of observations, the median is the value at the center position.
R Function: median()
```
median_value <- median(observations)
```

R Code Example

You can use the following R code to compute both mean and median:

# Define the observations
observations <- c(9, 5, 2, 3, 4, 6, 7)

# Calculate mean
mean_value <- mean(observations)

# Calculate median
median_value <- median(observations)

# Print the results
print(paste("Mean:", mean_value))
print(paste("Median:", median_value))

Results

Using the above R code, you’ll find:

Mean: $Mean = 7 ( 9 + 5 + 2 + 3 + 4 + 6 + 7 ) = 7 36 \approx 5.14$
Median: First, sort the data: (2, 3, 4, 5, 6, 7, 9). Since there are 7 values (an odd number), the median is the fourth value, which is 5.

Thus, the mean is approximately 5.14 and the median is 5.

17. Write a note on simple linear regression.

Simple linear regression is a statistical method used to model the relationship between two continuous variables: one independent variable (predictor) and one dependent variable (response). The goal is to find a linear equation that best predicts the dependent variable based on the independent variable’s values.

Objective of Simple Linear Regression:

The primary objectives are:

To determine the values of $β0\beta_0$ and $β1\beta_1$ that minimize the error between predicted and actual values of $Y$ .
To predict the value of the dependent variable $Y$ for a given value of $X$ .

Assumptions of Simple Linear Regression:

Linearity: The relationship between $X$ and $Y$ is linear.
Independence: The observations are independent of each other.
Homoscedasticity: The variance of the residuals (errors) is constant.
Normality: The residuals are normally distributed.

Example:

# Load built-in dataset
data(mtcars)

# Fit a simple linear regression model: Predict 'mpg' using 'wt'
model <- lm(mpg ~ wt, data = mtcars)

# View the summary of the model
summary(model)

# Predict values
predicted_values <- predict(model)

# Plot the regression line
plot(mtcars$wt, mtcars$mpg, main = "Simple Linear Regression", xlab = "Weight", ylab = "MPG")
abline(model, col = "blue")

Section - C

Answer any Two questions. Each question carries 10 marks. (2*10=20)

18. a) Discuss the features of R programming.

R is a well-developed, simple and effective programming language which includes conditionals, loops, user defined recursive functions and input and output facilities.
R has an effective data handling and storage facility.
R provides a suite of operators for calculations on arrays, lists, vectors and matrices.
R provides a large, coherent and integrated collection of tools for data analysis.
R provides graphical facilities for data analysis.

b) Explain the different algebraic operations on matrices.

Example:

# Create matrices
A <- matrix(1:6, nrow = 2, ncol = 3)
B <- matrix(7:12, nrow = 2, ncol = 3)

# Addition and Subtraction
C <- A + B
D <- A - B

# Element-wise Multiplication
E <- A * B

# Matrix Multiplication
C1 <- matrix(1:6, nrow = 3, ncol = 2)
D1 <- matrix(7:8, nrow = 2, ncol = 1)
F <- C1 %*% D1

# Transpose
G <- t(A)

# Inverse
H <- matrix(c(1, 2, 3, 4), nrow = 2)
H_inv <- solve(H)

# Determinant
det_H <- det(H)

# Eigenvalues and Eigenvectors
eig <- eigen(H)

# Print results
print("Matrix A:")
print(A)
print("Matrix B:")
print(B)
print("A + B:")
print(C)
print("A - B:")
print(D)
print("Element-wise multiplication A * B:")
print(E)
print("Matrix F (Dot product):")
print(F)
print("Transpose of A:")
print(G)
print("Inverse of H:")
print(H_inv)
print("Determinant of H:")
print(det_H)
print("Eigenvalues of H:")
print(eig$values)
print("Eigenvectors of H:")
print(eig$vectors)

19. a) Define variance, Covariance and correlation.

1. Variance

Variance measures the spread of a data set around its mean. It quantifies how much the data points deviate from the mean.

Formula for variance:
$Var(X)=∑(xi−xˉ)2n−1\text{Var}(X) = \frac{\sum (x_i – \bar{x})^2}{n – 1}$
where $xˉ\bar{x}$ is the mean of the data, and $n$ is the number of observations.
In R: Use the var() function to calculate the variance.

Example:

data <- c(10, 12, 14, 16, 18)
var(data)

Covariance measures the degree to which two variables move together. It indicates whether there is a positive or negative relationship between the variables.

Formula for covariance:
$Cov(X,Y)=∑(xi−xˉ)(yi−yˉ)n−1\text{Cov}(X, Y) = \frac{\sum (x_i – \bar{x})(y_i – \bar{y})}{n – 1}$
where $X$ and $Y$ are two variables, and $xˉ\bar{x}$ and $yˉ\bar{y}$ are their respective means.
In R: Use the cov() function to calculate covariance.

Example:

x <- c(2, 4, 6, 8, 10)
y <- c(1, 3, 5, 7, 9)
cov(x, y)

3. Correlation

Correlation measures the strength and direction of the linear relationship between two variables. It standardizes the covariance, producing values between -1 and 1:

-1: Perfect negative correlation
0: No correlation
1: Perfect positive correlation
Formula for correlation (Pearson correlation coefficient):
$Cor(X,Y)=Cov(X,Y)SD(X)⋅SD(Y)\text{Cor}(X, Y) = \frac{\text{Cov}(X, Y)}{\text{SD}(X) \cdot \text{SD}(Y)}$
In R: Use the cor() function to calculate the correlation.

Example:

x <- c(2, 4, 6, 8, 10)
y <- c(1, 3, 5, 7, 9)
cor(x, y)

b) Write a R program to illustrate plot ( ) list () and Pie ( ) plotting functions.

# Creating sample data for the plots
# Sample data for plot()
x <- 1:10 # x values
y <- c(2, 3, 5, 7, 11, 13, 17, 19, 23, 29) # y values (prime numbers)

# Sample data for pie chart
categories <- c("Category A", "Category B", "Category C", "Category D")
values <- c(10, 20, 30, 40) # Values corresponding to each category

# Create a plot using plot()
plot(x, y, type='b', col='blue', pch=19, lty=1,
main="Sample Plot", 
xlab="X-axis", 
ylab="Y-axis",
sub="Using plot() Function")

# Create a list to hold our data for demonstration
data_list <- list(X = x, Y = y, Values = values, Categories = categories)
print("Data List:")
print(data_list)

# Create a pie chart using pie()
# Adjusting the margins for better visualization
par(mar = c(1, 1, 1, 1)) # Set margins to zero

# Making the pie chart
pie(values, labels = categories, main = "Sample Pie Chart", col = rainbow(length(categories)))

# Restoring original par settings
par(mar = c(5, 4, 4, 2) + 0.1)

20. a) Explain the concept of Markov chain with a suitable example.

A Markov Chain is a mathematical system that undergoes transitions from one state to another within a finite or countable number of possible states. It is governed by the Markov Property, which states that the future state of a process depends only on its current state and not on its past history. This property implies that the process exhibits “memorylessness.”

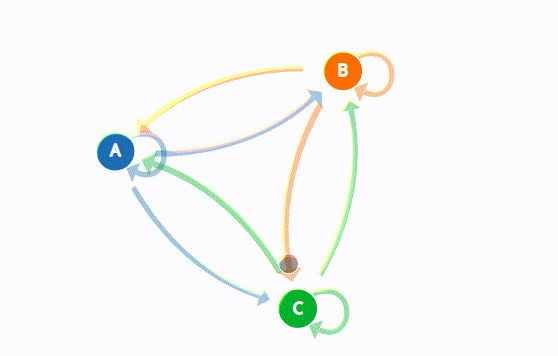
Key Components of Markov Chains

States: The distinct conditions or statuses that the process can occupy.
Transition Probabilities: The probabilities associated with moving from one state to another.
Initial State Distribution: The probability distribution over the states at the beginning of the process.

Mathematical Representation

A Markov Chain can be represented mathematically by a state transition matrix $P$ , where the entry $p_{ij}$ reflects the probability of transitioning from state $i$ to state $j$ . The rows of this matrix must sum to 1, as they represent probability distributions.

Example of a Markov Chain: Weather Prediction

To illustrate the concept of a Markov Chain, consider a simple weather prediction model with three states: Sunny (S), Cloudy (C), and Rainy (R).

States

State 1: Sunny
State 2: Cloudy
State 3: Rainy

b) Discuss the following:

i) Defining colors in R plots

1. Using Built-in Color Names

R has 657 predefined color names that can be used directly. You can access them using the colors() function.

2. Using RGB Colors

You can define custom colors using the RGB color model. The values for Red, Green, and Blue are specified on a scale from 0 to 1 or 0 to 255.

Syntax:

rgb(red, green, blue, alpha)

red, green, blue: Specify color intensity.
alpha: Specifies transparency (0 = fully transparent, 1 = opaque).

3. Using Hexadecimal Color Codes

Colors can be defined using hexadecimal notation. A hex color code has the format #RRGGBB or #RRGGBBAA where:

RR: Red
GG: Green
BB: Blue
AA: Transparency (optional)

4. Using Color Palettes

R provides several predefined color palettes to make plots visually appealing. Some popular palettes include:

rainbow(): Generates rainbow colors.
heat.colors(): Shades from red to yellow.
terrain.colors(): Shades of green and brown (terrain-like).
topo.colors(): Shades of blue and green (topographic).
cm.colors(): Cyan-magenta shades.

5. Transparency in Colors

Transparency can be added using the alpha parameter in rgb() or by specifying the alpha value in hex codes.

Hex with transparency: #RRGGBBAA (e.g., #FF573380 adds 50% transparency).

6. Color Brewer Palettes (Advanced Visualization)

For advanced color schemes, you can use the RColorBrewer package, which provides palettes for different types of data:

Sequential: For ordered data (e.g., gradients).
Diverging: For highlighting two extremes.
Qualitative: For categorical data.

ii) Point and click coordinate interaction.

The locator() function in base R provides a simple way to facilitate this point-and-click interaction.

Using locator()

The locator() function allows users to click on a plot and retrieve the (x, y) coordinates of the clicked points. Below, I’ll provide an example demonstrating how to create a plot and use point-and-click to get coordinates.

# Create a sample dataset
set.seed(1)
x <- rnorm(10) # Random normal values
y <- rnorm(10) # Random normal values

# Create a scatter plot
plot(x, y, pch = 19, col = "blue", main = "Click on Points", xlab = "X-axis", ylab = "Y-axis")

# Use locator() to capture points
cat("Click on the points in the plot. Press ESC when done.\n")

# Capture the coordinates of the clicks
clicked_points <- locator()

# Show the clicked coordinates
cat("You clicked the following coordinates:\n")
print(clicked_points)

RP Regular 2024 (NEP) Solved Question Paper Questions with Answers

Section - A

Answer any TEN questions. Each question carries 2 marks. (10*2=20)

1. List the basic datatypes in R.

2. Define list in R. Write an example to create a list.

3. What do you mean by special values ? Give example.

4. Mention the different assignment operators in R with examples.

5. Differentiate between cat ( ) and Print ( ) functions.

6. Write the syntax of “while” and “repeat” statements in R.

7. Write the purpose of prod ( ) and round ( ) functions. Give example for each.

8. List any four functions on set operations.

9. Define normal distribution.

10. What is ANOVA? Write the notations for Null and alternative hypothesis.

11. Write the purpose and syntax of Im ( ) function in R.

12. What are regions and margins in a R plot?

Section - B

Answer any FOUR from the following questions. Each question carries 5 marks. (4*5=20)

13. Define vector in R. Explain the different ways of creating a vector.

14. What is recursion? Write an R program to find the factorial of a number using recursion.

15. What is a file? Explain any four file handling functions in R.

16. Compute the mean and median for the following observations: (9,5,2,3,4,6,7) Mention the R functions for the same.

17. Write a note on simple linear regression.

Section - C

Answer any Two questions. Each question carries 10 marks. (2*10=20)

18. a) Discuss the features of R programming.

b) Explain the different algebraic operations on matrices.

19. a) Define variance, Covariance and correlation.

b) Write a R program to illustrate plot ( ) list () and Pie ( ) plotting functions.

20. a) Explain the concept of Markov chain with a suitable example.

b) Discuss the following:

i) Defining colors in R plots

ii) Point and click coordinate interaction.

Leave a ReplyCancel Reply

Pages

Help

About Us