Data Structure 2023 (Reg/Rep) NEP Solved Question Paper
Section - A
1. Answer any Six questions. (6 x 2= 12)
a) Define pointers Give syntax and example
In programming, a pointer is a variable that stores the memory address of another variable. Pointers are widely used in languages like C, C++, and other low-level languages.
Syntax:
data_type *pointer_name;
Example:
int main()
{
int num = 10;
int *ptr = # // ptr stores the memory address of num
printf("Value of num: %d\n", *ptr); // Output: Value of num: 10
return 0;
}b) Explain recursion with its types.
Recursion is a programming technique wherein a function calls itself directly or indirectly to solve a problem. When a function uses recursion, it breaks the problem into smaller subproblems of the same type.
Recursion has two main types:
Direct Recursion
Indirect Recursion
c) Differentiate singly and doubly linked list.
Singly Linked List:
- In a singly linked list, each element (node) contains data and a reference (or pointer) to the next node in the sequence.
- Traversal is only possible in one direction, from the first node through each subsequent node.
- Deletion of a node requires traversing the list and updating the links.
Doubly Linked List:
- In a doubly linked list, each element contains data as well as references to the next and previous nodes.
- Traversal is possible in both forward and backward directions.
- Deletion or insertion of a node is generally more efficient than in a singly linked list because the links in the surrounding nodes can be easily updated.
d) Explain sequential search with its advantages.
Sequential search, also known as linear search, is a method for finding a particular value in a list by checking each element in sequence until the desired element is found or the list is exhausted. The list can be unordered or ordered.
Here is the basic algorithm for sequential search:
- Start from the first element in the list.
- Compare the target value with the current element.
- If the current element matches the target, the search is successful.
- If not, move to the next element and repeat steps 2-3.
- Continue until the target is found or until the end of the list is reached.
Advantages of Sequential Search:
- Simplicity: The algorithm is straightforward and easy to implement.
- Applicability: It can be applied to any list, regardless of whether it’s ordered or unordered.
- Minimal processing overhead: There is no need to pre-process the list, making it ideal for small lists or situations where the list is constantly changing.
e) Define true and degree of a node.
True: In a directed graph, a node’s true refers to the total number of edges connected to it (both incoming and outgoing edges). In simpler terms, the true of a node is the sum of its indegree and outdegree.
Degree of a Node: The degree of a node in a graph is the number of edges incident to that node. For an undirected graph, the degree of a node is equal to the number of edges connected to it. In a directed graph, the degree can be split into two parts:
- Indegree: The number of edges directed into a node.
- Outdegree: The number of edges originating from a node and going out.
f) Define stack list some application of stack.
A stack is a linear data structure that follows the Last In, First Out (LIFO) principle. This means that the most recently added item is the first one to be removed.
A stack supports two main operations:
- Push: Adding an element to the top of the stack.
- Pop: Removing the top element from the stack.
Some applications of stacks include:
- Function Calls and Recursion
- Expression Evaluation
- Undo functionality in text editors
- Backtracking in algorithms
- Memory Management
g) Explain postfix expression with example.
A postfix expression, also known as a Reverse Polish Notation (RPN), is a mathematical notation in which every operator follows all of its operands. In other words, the operator is placed after the operands.
For example, the infix expression “3 + 4” would be expressed in postfix notation as “3 4 +”.
h) Define priority queue. Give its types.
A priority queue is an abstract data type that operates similar to a regular queue or stack, but where elements have a priority associated with them. In a priority queue, an element with a higher priority is served before an element with a lower priority. If two elements have the same priority, they are served according to their order in the queue.
Types of Priority Queue:
Max Priority Queue: In a max priority queue, elements with the highest priority are served first. For example, in a max priority queue of integers, the largest integer is served first.
Min Priority Queue: In a min priority queue, elements with the lowest priority are served first. For example, in a min priority queue of integers, the smallest integer is served first.
2. Answer any Three of the following. (3 x 4 =12)
a) Define data structure. Explain primitive and non-primitive data structure.
A data structure is a way of organizing and storing data so that it can be accessed and worked with efficiently. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data.
Primitive Data Structure: Primitive data structures are the fundamental data types that are supported directly by the programming language. These data types are built into the language and are considered as the basic building blocks for algorithm design. Examples of primitive data types include integers, floating-point numbers, characters, and Booleans. Primitive data structures are simple and are used to store a single value at a time.
Non-Primitive Data Structure: Non-primitive data structures are also known as abstract data types (ADTs). They are not defined by the programming language but are instead implemented using primitive data types. These structures are more complicated than primitive data structures as they can store and organize multiple data elements. Examples of non-primitive data structures include arrays, linked lists, stacks, queues, trees, graphs, and more. They are used to store and manage collections of data and come with predefined operations. Non-primitive data structures are more flexible and can store and manipulate complex data relationships.
b) Convert infix to prefix (xy) +z + M-N/(P * Q).
Converting an infix expression to a prefix expression involves rearranging the operators and operands to follow the prefix notation, where the operators precede their operands.
Given infix expression: (xy) + z + M – N / (P * Q)
Step 1: Reverse the infix expression
(P * Q) / N – M + z + (xy)
Step 2: Convert the reversed infix expression to postfix expression.
The infix expression’s postfix equivalent is: PQ* N / M – z + xy +
Step 3: Reverse the postfix expression to get the prefix expression.
The final prefix expression is: + + – / * P Q N M z xy
Therefore, the infix expression (xy) + z + M – N / (P * Q) can be converted to the prefix expression + + – / * P Q N M z xy.
c) Write a program to find GCD of two numbers.
Using Python
def gcd(a, b):
while b != 0:
a, b = b, a % b
return a
# Taking input from the user
num1 = int(input("Enter first number: "))
num2 = int(input("Enter second number: "))
# Printing the GCD of the two numbers
print("The GCD of", num1, "and", num2, "is", gcd(num1, num2))
Using C
#include <stdio.h>
int gcd(int a, int b)
{
while (b != 0)
{
int temp = b;
b = a % b;
a = temp;
}
return a;
}
int main()
{
int num1, num2;
printf("Enter first number: ");
scanf("%d", &num1);
printf("Enter second number: ");
scanf("%d", &num2);
printf("The GCD of %d and %d is %d\n", num1, num2, gcd(num1, num2));
return 0;
}d) Explain tower of hanoi problem with example.
The Tower of Hanoi is a classic problem in computer science and mathematics. It consists of three rods and a number of disks of different sizes that can slide onto any rod. The puzzle starts with the disks stacked in ascending order of size on one rod, with the smallest disk at the top, making a conical shape. The objective is to move the entire stack to another rod, following these rules:
- Only one disk can be moved at a time.
- Each move consists of taking the top disk from one stack and placing it on top of another stack.
- No disk may be placed on top of a smaller disk.
Here’s a C program to solve the Tower of Hanoi problem
#include<stdio.h>
int main()
{
int n;
char s, d, a;
s='s';
d='D';
a='A';
printf("\n Enter number of disc : ");
scanf("%d", &n);
towers(n, s, a, d);
}
void towers(int n, char s, char a, char d)
{
if(n==1)
{
printf("\n\n Move %d disc from %c to %c ", n,s,d);
return;
}
towers(n-1,s,d,a);
printf("\n\n Move %d disc from %c to %c ", n,s,d);
towers(n-1,a,s,d );
}
3. Answer any Three questions of the following. (3x4=12)
a) Explain Iterative and Recursive function.
Iterative Functions
An iterative function uses a loop (like for, while, or do-while) to repeatedly execute a block of code until a certain condition is met. This approach is often more intuitive and efficient for simple problems.
Example: Calculating factorial using iteration:
int factorial_iterative(int n)
{
int result = 1;
for (int i = 2; i <= n; i++)
{
result *= i;
}
return result;
}
int factorial_recursive(int n)
{
if (n == 0 || n == 1)
{
return 1;
} else {
return n * factorial_recursive(n - 1);
}
}b) write 'C' program to generate Fibonacci series using recursion.
#include<stdio.h>
int fib(int n);
int main()
{
int n, i;
printf("\n Enter fibonacci numbers : ");
scanf("%d",&n);
printf("\n");
for(i=1; i<=n; i++)
{
printf("%d\t",fib(i));
}
return 0;
}
int fib(int n)
{
if(n==1)
{
return 0;
}
if(n==2)
{
return 1;
}
else
{
return fib(n-1)+fib(n-2);
}
}
#include <stdio.h>
int fibonacci(int n)
{
if (n <= 1)
return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}
int main()
{
int n, i;
printf("Enter the number of terms for Fibonacci series: ");
scanf("%d", &n);
printf("Fibonacci Series: ");
for (i = 0; i < n; i++)
{
printf("%d, ", fibonacci(i));
}
return 0;
}c) Explain quick sort with example.
Quick Sort is a popular sorting algorithm that follows the Divide and Conquer strategy. It works by selecting a pivot element from the array and partitioning the other elements into two sub-arrays according to whether they are less than or greater than the pivot. The sub-arrays are then recursively sorted.
Example:
#include <stdio.h>
void swap(int* a, int* b)
{
int t = *a;
*a = *b;
*b = t;
}
int partition(int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high - 1; j++)
{
if (arr[j] < pivot)
{
i++;
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
void quickSort(int arr[], int low, int high) {
if (low < high)
{
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof(arr) / sizeof(arr[0]);
quickSort(arr, 0, n - 1);
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
return 0;
}
d) Write an algorithm to delete elements in arrays.
Input: The array
arr[], the lengthnof the array, and the elementelementto be deleted.Find the Element: Search for the element in the array that you want to delete. If the element is not found, exit and display an appropriate message.
Shift Elements: Once the element is found, shift all elements to the right of the selected element one position to the left to overwrite the element to be deleted.
Update Array Size: Decrease the array size by one (i.e.,
n = n - 1).
#include <stdio.h>
int findElement(int arr[], int n, int key);
int deleteElement(int arr[], int n, int key)
{
// Find position of element to be deleted
int pos = findElement(arr, n, key);
if (pos == -1)
{
printf("Element not found");
return n;
}
// Deleting element
int i;
for (i = pos; i < n - 1; i++)
arr[i] = arr[i + 1];
return n - 1;
}
// Function to implement search operation
int findElement(int arr[], int n, int key)
{
int i;
for (i = 0; i < n; i++)
if (arr[i] == key)
return i;
return -1;
}
int main()
{
int i;
int arr[] = { 10, 50, 30, 40, 20 };
int n = sizeof(arr) / sizeof(arr[0]);
int key = 30;
printf("Array before deletion\n");
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
// Function call
n = deleteElement(arr, n, key);
printf("\nArray after deletion\n");
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
return 0;
}
4. Answer any Three questions of the following. (3 x 4= 12)
a) Explain stack operations with example.
Stack is a fundamental data structure that follows the Last In, First Out (LIFO) principle. It supports two primary operations: push and pop.
Push Operation: The push operation adds an element to the top of the stack. It increases the stack’s size by one and places the new element at the top.
Pop Operation: The pop operation removes and returns the top element of the stack. It decreases the stack’s size by one.
Operations on Stack Data Structure:
In order to make manipulations in a stack.
- push() to insert an element into the stack
- pop() to remove an element from the stack
- top() Returns the top element of the stack.
- isEmpty() returns true if stack is empty else false.
- isFull() returns true if the stack is full else false.
#include<stdio.h>
#include<stdlib.h>
#define STACKSIZE 5
void push(int ele);
void pop();
void display();
int a[100];
int top = -1;
int main()
{
int choice,data,option;
do
{
printf("\n\n\tSTACK OPERATIONS");
printf("\n\n1.Push\t2.Pop\t3.Display\t4.Exit : ");
scanf("%d",&choice);
switch(choice)
{
case 1: printf("\n\nEnter Element to be Pushed : ");
scanf("%d",&data);
push(data);
break;
case 2: pop();
break;
case 3: display();
break;
case 4: printf("\n\nProgram is exiting....");
exit(0);
break;
default: printf("\n\nInvalid Choice..");
break;
}
printf("\n\nDo You Want t Continue?? Press 1 / 0 : ");
scanf("%d", &option);
}while(option == 1);
return 0;
}
void push(int ele)
{
if(top == STACKSIZE-1)
{
printf("\n\n**************STACK OVERFLOW**********\n\n");
return;
}
top = top + 1;
a[top] = ele;
printf("\n\nElement %d Pushed",ele);
}
void pop()
{
int var;
if(top == -1)
{
printf("\n\n*************STACK UNDERFLOW************\n\n");
return;
}
var = a[top];
top = top - 1;
printf("\n\nElement %d is Popped",var);
}
void display()
{
int i;
if(top == -1)
{
printf("\n\n*****STACK UNDERFLOW**************\n\n");
return;
}
printf("\n\n*****STACK ELEMENTS : ");
for(i=top; i>=0;i--)
{
printf("%d\t", a[i]);
}
}
b) Explain working of queue.
- Enqueue Operation: The enqueue operation adds an element to the rear of the queue. It increases the queue’s size by one and places the new element at the end.
- Dequeue Operation: The dequeue operation removes and returns the front element of the queue. It decreases the queue’s size by one.
- Front: Points to the first element in the queue.
- Rear: Points to the last element in the queue.
- Enqueue: Adds an element to the rear of the queue.
- Dequeue: Removes an element from the front of the queue.
- Peek: Returns the value of the front element without removing it.
- isEmpty: Checks if the queue is empty.
- isFull: Checks if the queue is full (in case of fixed-size implementation).
- Simple Queue
- Circular Queue
- Priority Queue
- Double-Ended Queue (Deque)
c) Convert the following expression to postfix notation.
i) (A * (B+C))/(D)-F
(A * (B + C)) / D – F
- Infix: (A * (B + C)) / D – F
- Postfix:
ABC+∗D/F−
ii) (x+y) * (m/n+d)
(x + y) * (m / n + d)
- Infix: (x + y) * (m / n + d)
- Postfix:
xy+mn/d+∗
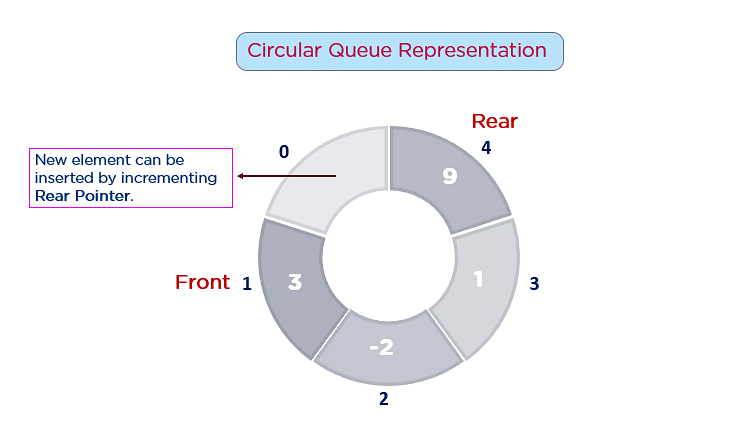
d) Explain circular queue with example.
A circular queue is a data structure that uses a single, fixed-size array to implement a queue with a circular shape.
It has a front and rear pointer that point to the front and rear elements of the queue, respectively. When elements are dequeued from the front, the front pointer advances, and when elements are enqueued at the rear, the rear pointer advances.
Working Principle of Circular Queue:
Empty Queue:
- Initially, both front and rear are set to -1 to indicate an empty queue.
Enqueue Operation (Insertion):
- At the rear pointer, element insertion occurs, and the rear pointer is updated.
- If the rear pointer reaches the end of the array, it wraps around to the beginning (making it circular).
- If the queue is full, it may overflow and a condition known as “queue full” occurs.
Dequeue Operation (Deletion):
- At the front pointer, element removal occurs, and the front pointer is updated.
- If the front pointer reaches the end of the array, it wraps around to the beginning (making it circular).
- If the queue is empty, a condition known as “queue empty” occurs.
// Circular Queue implementation in C
#include <stdio.h>
#define SIZE 5
int items[SIZE];
int front = -1, rear = -1;
int isFull() {
if ((front == (rear + 1) % SIZE) || (front == 0 && rear == SIZE - 1)) return 1;
return 0;
}
int isEmpty() {
if (front == -1) return 1;
return 0;
}
void enQueue(int element) {
if (isFull())
printf("\n Queue is full!! \n");
else {
if (front == -1) front = 0;
rear = (rear + 1) % SIZE;
items[rear] = element;
printf("\n Inserted -> %d", element);
}
}
int deQueue() {
int element;
if (isEmpty()) {
printf("\n Queue is empty !! \n");
return (-1);
} else {
element = items[front];
if (front == rear) {
front = -1;
rear = -1;
}
else {
front = (front + 1) % SIZE;
}
printf("\n Deleted element -> %d \n", element);
return (element);
}
}
void display() {
int i;
if (isEmpty())
printf(" \n Empty Queue\n");
else {
printf("\n Front -> %d ", front);
printf("\n Items -> ");
for (i = front; i != rear; i = (i + 1) % SIZE) {
printf("%d ", items[i]);
}
printf("%d ", items[i]);
printf("\n Rear -> %d \n", rear);
}
}
int main() {
// fails because front = -1
deQueue();
enQueue(1);
enQueue(2);
enQueue(3);
enQueue(4);
enQueue(5);
// fails to enqueue because front == 0 && rear == SIZE - 1
enQueue(6);
display();
deQueue();
display();
enQueue(7);
display();
// fails to enqueue because front == rear + 1
enQueue(8);
return 0;
}
5. Answer any Three questions of the following. (3x 4=12)
a) Explain how insertions and deletions performed in linked list.
In a linked list, insertions and deletions are fundamental operations that manipulate the structure of the list by adding or removing elements.
Insertions in a Linked List:
Inserting at the Beginning:
Create a new node with the given value.
Set the new node’s next pointer to the current head of the list.
Update the head of the list to point to the new node.
Inserting at the End:
Create a new node with the given value.
Traverse the list to find the last node.
Set the next pointer of the last node to the new node.
Inserting at a Specific Position:
Traverse the list to find the node at the desired position.
Adjust the pointers to insert the new node in the appropriate position.
Deletions in a Linked List:
Deleting at the Beginning:
Update the head of the list to point to the next node, effectively removing the first node.
Deleting at the End:
Traverse the list to find the node before the last node.
Set the next pointer of the second-to-last node to NULL, effectively removing the last node.
Deleting a Specific Node:
Traverse the list to find the node to be deleted and the node before it.
Adjust the pointers of the previous node to bypass the node to be deleted.
b) Define the following.
i) Depth ii) Path iii) Sibling
i) Depth: The depth of a node in a tree is the length of the path from the root to that specific node. The depth of the root node is typically considered 0. As you move away from the root, the depth of the nodes increases by 1 for each level. The depth of a node indicates how many edges are in the longest path from the node to the root.
ii) Path: A path in a tree is a series of nodes where each node is connected to the next node in the sequence by an edge. This sequence traces a route from one node to another within the tree structure. A path could be from the root node to any other node in the tree or between any two nodes within the tree.
iii) Sibling: Siblings in a tree are nodes that share the same parent node. If two nodes have the same parent node, they are considered siblings. Siblings are on the same level in the tree hierarchy, meaning they are children of the same parent node. Understanding siblings is crucial for analyzing the relationship between nodes in a tree.
c) Define
i) Heap tree. ii) Doubly linked list. iii) Strict binary tree.
i) Heap Tree: A “heap” is a specialized tree-based data structure that satisfies the heap property. This property could represent either a “max-heap” where the value of each node is greater than or equal to the values of its children or a “min-heap” where each node is smaller than or equal to its children. A heap is typically used to implement priority queues and is commonly represented as an array. In a heap, the highest (or lowest) priority element is always stored at the root.
ii) Doubly Linked List: A doubly linked list is a type of linked list where each node contains a data part and two pointers. These pointers allow traversal in both forward and backward directions – one points to the next node and the other to the previous node. This bidirectional feature facilitates efficient insertion, deletion, and traversal.
iii) Strict Binary Tree: A strict binary tree, also known as a proper binary tree, is a type of binary tree in which each node has either 0 or 2 children. In other words, each node in a strict binary tree must have 0 or 2 children; having only one child is not allowed. This concept is fundamental in areas such as data structuring and algorithm design due to its balanced and organized structure.
d) Write an algorithm to display post order traversal of a binary tree.
#include <stdio.h>
#include <stdlib.h>
{
int data;
struct Node *left;
struct Node *right;
};
// Create a new node
struct Node* createNode(int value)
{
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = value;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// Perform post-order traversal
void postOrderTraversal(struct Node* root)
{
if (root == NULL) {
return;
}
postOrderTraversal(root->left);
postOrderTraversal(root->right);
printf("%d ", root->data);
}
int main()
{
// Create a sample binary tree
struct Node* root = createNode(1);
root->left = createNode(2);
root->right = createNode(3);
root->left->left = createNode(4);
root->left->right = createNode(5;
// Display the post-order traversal of the binary tree
printf("Post-order traversal of the binary tree: ");
postOrderTraversal(root);
return 0;
}