DAA Repeater 2023 (CBCS) Solved Question Paper Questions with Answers
Section - A
Answer any ten questions. (10x2=20)
1. a) Define algorithm.
- An algorithm is a step – step procedure used for calculations, problem-solving, and decision making.
- It is a finite sequence of well-defined, unambiguous instructions to achieve a particular outcome.
An algorithm is a procedure used for solving a problem or performing a computation. Algorithms act as an exact list of instructions that conduct specified actions step by step in either hardware- or software-based routines.
b) Write a pseudo code convention for while loop.
while (Condition)
{
//code clock
//code condition
}
c) Define space and time complexity of an algorithm.
Space complexity: The amount of memory. Space required by an algorithm to execute.
Time complexity: The amount of time taken by on algorithm to complete its execution.
Space complexity: Space complexity refers to the amount of memory space an algorithm requires to solve a problem, including the space used by the input values, temporary variables, and the space needed for the algorithm itself.
Time complexity: Time complexity represents the amount of time an algorithm takes to solve a problem as a function of the length of its input. It measures the number of operations or steps an algorithm requires to complete its execution.
d) Define divide and conquer method.
Divide of Conquer is a problem-solving. strategy where a problem is divided into Smaller sub-problems that are solved recursively.
The Divide-and-Conquer method is a problem-solving strategy widely used in computer science and mathematics. It involves breaking down a complex problem into smaller, more manageable subproblems, solving each subproblem independently, and then combining the solutions to solve the original problem.
e) Write the differences between straight maxmin and recursive maxmin algorithm.
Straight Maxmin Algorithm:
- Operates in a linear manner, evaluating each possible move sequentially.
- Follows a systematic approach by considering each move at a given depth before proceeding to the next level.
- Computes the best move based on the outcome of evaluating all possible moves at each depth, without backtracking.
- Can be less resource-intensive compared to recursive algorithms for shallower depths.
Recursive Maxmin Algorithm:
- Utilizes a recursive approach, allowing for backtracking and deeper exploration of the game tree.
- Evaluates possible moves by recursively calling the algorithm on subsequent game states, analyzing possible outcomes.
- Involves depth-first search to explore the game tree until a specific depth or terminal state is reached.
- Tends to be more computationally intensive but can provide more optimal solutions for complex games.
f) Define feasible and optimal solution.
Feasible Solution:
- A feasible solution refers to a solution that satisfies all given constraints or requirements within a specific problem or system.
- It is a solution that is viable, possible, and can be implemented without violating any constraints or conditions.
Optimal Solution:
- An optimal solution is the best possible solution among all feasible solutions, typically in the context of optimization problems.
- It represents the most favorable outcome in terms of maximizing or minimizing a specific objective, such as maximizing profit, minimizing cost, or optimizing performance.
g) Differentiate between dynamic programming and greedy method.
| Dynamic Programming | Greedy Method |
| Breaks down problems into simpler subproblems and solves each once | Selects the best immediate solution at each step |
| Focuses on solving all subproblems optimally and combining them | Provides a locally optimal solution without reassessment |
| Guarantees an optimal solution by considering all subproblems | Does not ensure globally optimal solutions |
| Involves backtracking and storing solutions for efficient computation | Does not backtrack or reevaluate decisions once made |
| Tends to have higher time complexity due to solving all subproblems | Often simpler and faster due to straightforward decision-making |
| Ideal for problems with optimal substructure and overlapping subproblems | Suitable for problems with greedy choice properties |
h) What do you mean by two way merge pattern?
The two-way merge pattern, also known as binary merging, refers to a technique for merging two already sorted lists into a single sorted list. It’s a fundamental step used in various sorting algorithms like merge sort.
The two-way merge pattern, also known as the merge algorithm, is a sorting technique commonly used in merge sort algorithms. In this pattern:
Divide
Merge
Repeat
The two-way merge pattern ensures that the sorting process is efficient by breaking down the list into smaller sublists for sorting and then successively merging them into larger, sorted sublists until the entire list is sorted. This pattern is a fundamental component of merge sort algorithms and contributes to their efficiency and effectiveness in sorting large datasets.
i) Define tree traversal.
In Design and Analysis of Algorithms (DAA), tree traversal refers to the process of visiting and exploring all the nodes of a tree data structure in a systematic manner. There are mainly three types of tree traversal techniques:
Inorder Traversal:
- In inorder traversal, the nodes are visited in the following order: left child, root, right child.
- This traversal technique is commonly used in binary search trees to retrieve data in sorted order.
Preorder Traversal:
- Preorder traversal visits the nodes in the following order: root, left child, right child.
- This traversal method is useful for creating a copy of the tree or prefix expression evaluation.
Postorder Traversal:
- Postorder traversal involves visiting the nodes in the following order: left child, right child, root.
- This traversal approach is often used in deleting a tree or evaluating postfix expressions.
Tree traversal is essential in algorithms that require processing or accessing all the nodes of a tree, such as searching for a specific node, modifying tree structure, or performing various operations on the tree elements. Different traversal techniques offer unique ways to navigate through the tree, resulting in different sequences of visiting nodes based on the traversal method used.
j) Differentiate between directed graph and undirected graph, with neat diagram.
Directed Graph:
- Definition: In a directed graph, the edges have a direction associated with them, indicating one-way relationships between nodes.
- Representation: The edges are represented by arrows, signifying the direction of the relationship.
- Example: An arrow from node A to node B implies a directed edge from A to B, meaning a connection or relationship exists only from A to B, not necessarily in the opposite direction
A
/ \
/ \
v >
B C
^ /
\ /
\ /
D
Undirected Graph:
- Definition: In an undirected graph, the edges do not have a direction associated with them, indicating bidirectional relationships between nodes.
- Representation: The edges are represented by lines connecting nodes, signifying relationships that work in both directions.
- Example: A line connecting node X and Y implies an undirected edge between X and Y, indicating a mutual connection between the nodes.
A------B
\ /
\ /
\/
Ck) Define Hamiltonian cycle.
A Hamiltonian Cycle is a concept in graph theory that refers to a closed loop or cycle in a graph that visits every vertex once and returns to the starting vertex without visiting any vertex more than once, except for the starting vertex.
l) For the given graph, state the in degree and out degree of node 1 and 2

Node 1:
- In-Degree: 2 (Incoming edges from Node 3 and Node 4)
- Out-Degree: 1 (Outgoing edge to Node 2)
Node 2:
- In-Degree: 1 (Incoming edge from Node 1)
- Out-Degree: 0
Out Degree:
Vertex 1 : 1
Vertex 2 : 1
Vertex 3 : 0
In Degree:
Vertex 1 : 1
Vertex 2 : 1
Vertex 3 : 1
Section - B
Answer any four questions. (4x5=20)
2. Explain characteristics of an algorithm.
- Correctness: An algorithm should produce the correct output for all possible valid inputs.
- finiteness: An algorithm must terminate of after a finite number of steps.
- Definiteness: Each step of the algorithm Should be Precisely defined & unambiguous leaving no room for interpretation.
- Input: An algorithm may take input data which is processed to produce the desired Output.
- Output: An algorithm produces output based on the input provided and the. Operations performed during execution.
- Clarity: An algorithm should be easy to understand and implement.
3. Explain asymptotic notations.
1. Big O Notation:
Big O notation represents the upper bound on worst-case Scenario of the growth rate of a function on the resource usage of an algorithm.

2. Omega Notation:
Omega notation represent the lower bound as best case scenario of the growth rate of a function or the recourse usage of an algorithms.

3. Theta Notation:
It represents both upper & lower bounds of the growth rate of a function or the resource usage of an algorithm.

4. Explain Binary search algorithm in detail.
function binary Search (array, Target)
low=0
high = len (array) - 1
while low <= high:
mid = (low-thigh) 1/2
if array [mid] == target:
return mid
elif array [mid] < target:
low = mid + 1
else:
high = mid - 1
return -1 #element not found
- “array” is the sorted being searched.
- “target” is the value being searched.
- “left “right” represents the current boundaries of the search interval.
- “mid” is the index of the middle element of the wind search interval.
The Binary Search algorithm is an efficient search algorithm that is used to find the position of a target value within a sorted array.
Binary Search Algorithm:
Initialization:
Begin with a sorted array of elements.
Set a low pointer at the start of the array (usually 0) and a high pointer at the end of the array (length of the array – 1).
Search Process:
Calculate the middle index mid as (low + high) / 2.
Compare the target value with the element at the middle index (array[mid]):
If the target value matches the middle element, the search is successful, and return the index.
If the target is less than the middle element, update the high pointer to mid – 1 and repeat the process in the lower half of the array.
If the target value is greater than the middle element, update the low pointer to mid + 1 and repeat the process in the upper half of the array.
Repeat this process until the target value is found or until the low pointer is greater than the high pointer.
Termination:
If the target value is not found after the search process, return a “value not found” indicator.
Example:
Let’s apply the Binary Search algorithm to find the position of the target value 8 in the sorted array: [2, 4, 6, 8, 10, 12, 14, 16, 18, 20].
Initial State:
low = 0, high = 9
mid = (0 + 9) / 2 = 4
Array: [2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
Compare array[mid] (10) with the target value (8).
Since 8 is less than 10, update high = mid – 1 = 3 and continue the process in the lower half.
Next State:
low = 0, high = 3
mid = (0 + 3) / 2 = 1
Array: [2, 4, 6, 8]
Compare array[mid] (4) with the target value (8).
Since 8 is greater than 4, update low = mid + 1 = 2 and continue in the upper half.
Final State:
low = 2, high = 3
mid = (2 + 3) / 2 = 2
Array: [6, 8]
Compare array[mid] (8) with the target value (8).
The target value (8) matches the middle element, so the position is found. Return the index 3 as the target value 8 is found at the 4th position in the array with 0 indexing.
5. Using the greedy knapsack algorithm find optimal solution for following, n=7, m= 20
(P1 to P2) = (10,5,15,7,6,18,3)
(W1 to W2) = (2,3,5,7,1,4,1)
To find the optimal solution using the Greedy Knapsack Algorithm, where n=7, m=20, and we have the following profits (P1 to P2) = (10, 5, 15, 7, 6, 18, 3) and weights (W1 to W2) = (2, 3, 5, 7, 1, 4, 1), we can follow these steps:
Greedy Knapsack Algorithm:
Calculate Profit-to-Weight Ratio:
- Calculate the profit-to-weight ratio for each item by dividing the profit by the weight. This will help in determining the most profitable items relative to their weight.
Sort Items:
- Sort the items based on their profit-to-weight ratio in descending order. This step allows us to prioritize items with higher profitability relative to their weight.
Select Items:
- Begin selecting items starting from the highest profit-to-weight ratio while ensuring that the cumulative weight of the selected items doesn’t exceed the capacity of the knapsack (m=20).
- Keep adding items until the cumulative weight exceeds the knapsack capacity or all items are considered.
Optimal Solution:
- The selected items will form the optimal solution maximizing the total profit within the weight capacity constraint.
Calculation:
- Profit-to-Weight Ratios: [(10/2), (5/3), (15/5), (7/7), (6/1), (18/4), (3/1)] = [5, 1.67, 3, 1, 6, 4.5, 3]
- Sorted Profit-to-Weight Ratios: [6, 5, 4.5, 3, 3, 1.67, 1]
- Sorting the items based on the ratios gives us the following order (P, W): [(18, 4), (10, 2), (15, 5), (3, 1), (7, 7), (6, 1), (5, 3)]
- Starting with the highest ratio item: (18, 4), (10, 2), (15, 5), and (3, 1) would fill the knapsack to the total weight of 12 and total profit of 46.
6. Write a algorithm to find all pairs of shortest path.
To find all pairs of shortest paths in a graph, you can use the Floyd-Warshall algorithm. The Floyd-Warshall algorithm finds the shortest path for all pair of vertices in a weighted graph. Below is the pseudocode for the Floyd-Warshall algorithm:
function FloydWarshall(graph):
// Initialize distance matrix with the graph's weights
let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity)
for each vertex v in graph:
dist[v][v] = 0 // Distance to itself is 0
for each edge (u, v) in graph:
dist[u][v] = weight of edge (u, v) // Distance to adjacent vertices
// Calculate all pairs shortest paths
for k from 1 to |V|: // Intermediate vertex
for i from 1 to |V|: // Source vertex
for j from 1 to |V|: // Destination vertex
if dist[i][k] + dist[k][j] < dist[i][j]: // If a shorter path exists
dist[i][j] = dist[i][k] + dist[k][j] // Update the shortest path
return dist // Distance matrix containing all pairs shortest paths
The above pseudocode describes the Floyd-Warshall algorithm to find all pairs of shortest paths in a graph. After running the algorithm, the dist matrix will contain the shortest paths between all pairs of vertices in the graph.
The time complexity of the Floyd-Warshall algorithm is O(V^3), where V is the number of vertices in the graph. This makes it very efficient for finding all pairs of shortest paths in dense graphs.
7. Write a note on sum of sub set problem.
Sum of Subset Problem:
The Subset Sum Problem is a classic problem in computer science and mathematics involving finding a subset of elements in an array that adds up to a given target sum. This problem falls under the category of combinatorial optimization problems and can be solved through various techniques.
Problem Statement:
Given a set of positive integers and a target sum, the task is to determine whether there exists a subset with a sum equal to the target sum.
Example:
Consider the set: [3, 34, 4, 12, 5, 2] and the target sum: 9. The problem demands to find if there is a subset whose elements sum up to 9.
Applicability:
The Sum of Subset Problem finds applications in various domains such as finance, resource allocation, cryptography, and data mining. It serves as a foundation for addressing complex numerical problems including cryptographic key exchange, portfolio optimization, and more.
Techniques to Solve:
Brute Force Approach: It involves generating all possible subsets and checking their sum against the target sum. Although simple, this approach becomes impractical for large sets due to its exponential time complexity.
Dynamic Programming: The problem can be efficiently solved using the dynamic programming technique. The approach efficiently uses memoization to store the information about the subsets already considered, thereby reducing redundant calculations.
Backtracking: Another method involves using backtracking to explore different combinations and eliminate configurations that don’t satisfy the target sum criterion.
Section - C
Answer any four full questions. (4*10=40)
8. Explain the various pseudo code conventions for specifying algorithm.
Pseudo Code Conventions for Specifying Algorithms
Naming Conventions
- Choose descriptive variable and function names.
- Use camelCase or underscores for multi-word names.
Comments
- Begin each section with a comment explaining its purpose.
- Use comments to clarify complex or non-intuitive sections of code.
Variables
- Declare variables with a clear type and purpose.
- Initialize variables before use.
Control Structures
- Use standard control structures like if-else, while, for, etc.
- Indent code within control structures for readability.
Functions and Procedures
- Define functions and procedures for repeating tasks.
- Include a clear description of input parameters and return values.
Input and Output
- Clearly specify input and output parameters and their usage.
Error Handling
- Include error handling for possible exceptions or invalid inputs.
Formatting and Indentation
- Use consistent indentation for improved readability.
- Format the code to keep it visually organized and easy to follow.
9. a) Write a note on strassen’s matrix multiplication.
Strassen’s Matrix Multiplication
Strassen’s algorithm is an efficient method to multiply two matrices using divide-and-conquer techniques. It aims to reduce the number of multiplications required for matrix multiplication, ultimately improving the overall computational efficiency. Here are key points to note about Strassen’s matrix multiplication:
Algorithm Overview:
- Instead of the traditional matrix multiplication method that requires 8 multiplications for each cell, Strassen’s algorithm reduces this to 7 multiplications by using a clever recursive approach.
Divide-and-Conquer Approach:
- Strassen’s algorithm divides each matrix into submatrices, performs recursive multiplications of these submatrices, and then combines the results to obtain the final matrix product.
Efficiency:
- While Strassen’s algorithm reduces the number of multiplications needed, it increases the number of additions and subtractions. However, for large matrices, the reduction in multiplications leads to overall performance improvement.
Complexity:
- The time complexity of Strassen’s algorithm is O(n^log2(7)), which is approximately O(n^2.81). This makes it more efficient than the traditional O(n^3) method for large matrices.
Applicability:
- Strassen’s algorithm is particularly useful when dealing with large matrices where the reduction in multiplications significantly impacts the overall computation time.
Limitations:
- Strassen’s algorithm is not efficient for small matrices due to the overhead of the additional additions and subtractions involved. Therefore, it is generally most effective for matrices of a certain size or larger.
b) Sort the following array using quick sort a {1:8} 5,3,1,4,8,2,9,7.
def partition(data, low, high):
pivot = data[high]
i = low - 1
for j in range(low, high):
if data[j] <= pivot:
i += 1
data[i], data[j] = data[j], data[i]
data[i + 1], data[high] = data[high], data[i + 1]
return i + 1
def quick_sort(data, low, high):
if low < high:
pi = partition(data, low, high)
quick_sort(data, low, pi - 1)
quick_sort(data, pi + 1, high)
# Driver code
data = [5, 3, 1, 4, 8, 2, 9, 7]
n = len(data)
quick_sort(data, 0, n - 1)
print("Sorted array in ascending order:", data)
10. a) Find shortest path and its length from source vertex 1 to all the destinations for the given graph.
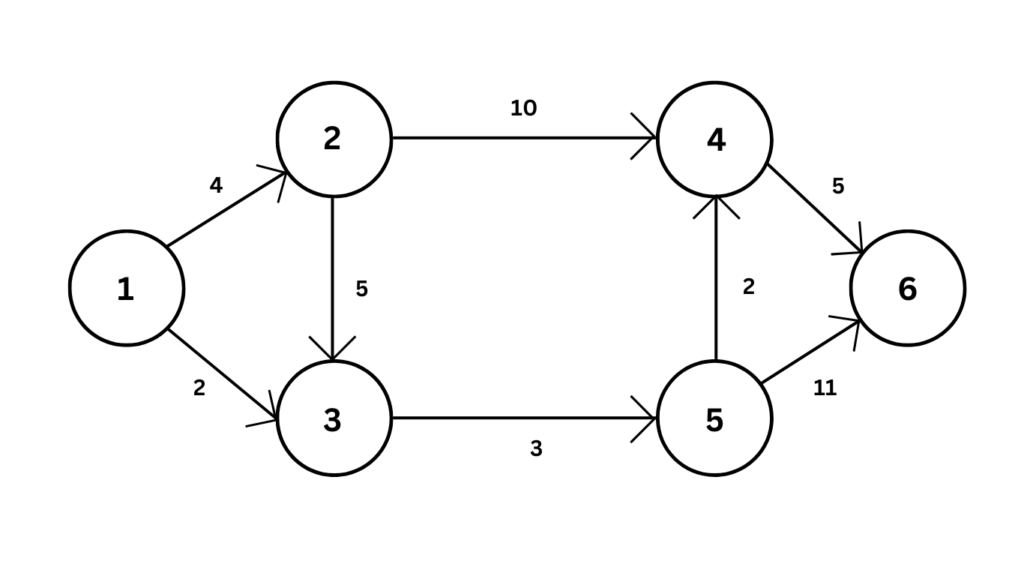
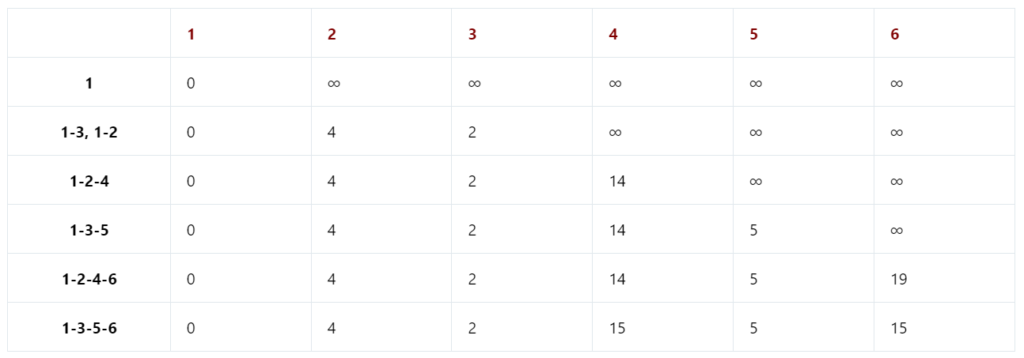
b) Find the minimum cost spanning tree using prims algorithm.
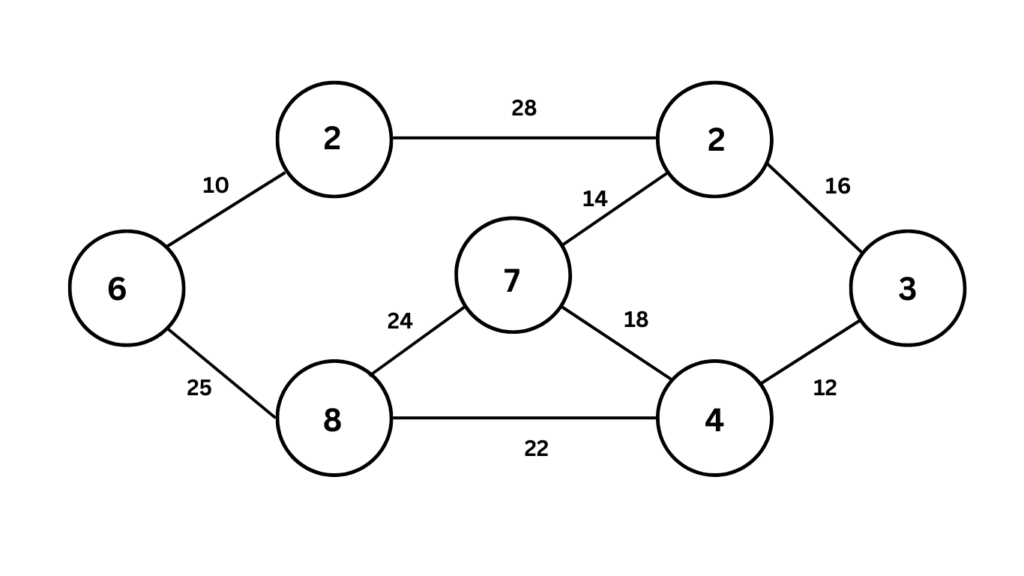
Prim’s algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted connected undirected graph. A minimum spanning tree is a subset of edges that connects all vertices in the graph with the lowest possible total edge weight. Here’s how Prim’s algorithm works:
- Choose a starting vertex: You can arbitrarily choose any vertex in the graph as the starting vertex.
- Mark all vertices unvisited: Initialize a set to keep track of visited vertices. Initially, all vertices are marked unvisited.
- Include the cheapest edge in the MST: Find the edge with the minimum weight that connects a vertex in the MST set to a vertex not in the MST set. Add this edge to the minimum spanning tree and mark the newly included vertex as visited.
- Repeat steps 3 and 4: Continue finding the cheapest edge that connects a visited vertex to an unvisited vertex until all vertices are included in the MST.
Following these steps on the graph in the image, we get the following minimum spanning tree with a total cost of 35:
22
/ \
2 12
/ \ \
8 3 4
/ \ \
6 24 14
\ \ /
7 18 10
/ \
25 2811. a) Write a note on 4x4 queen’s problem.
4×4 Queens Problem:
The 4×4 Queens Problem is a specific instance of the N-Queens Problem, where the objective is to place 4 queens on a 4×4 chessboard such that no two queens threaten each other. This problem serves as a small-scale representation of the classic N-Queens Problem, enabling the exploration of all possible solutions within a manageable search space.
Key Characteristics:
Problem Size:
- In the 4×4 Queens Problem, the 4×4 chessboard provides a compact and comprehensible problem space, allowing for the exhaustive examination of all possible queen placements.
Search Space:
- The 4×4 grid results in a limited search space, facilitating the systematic exploration of all valid configurations and the demonstration of backtracking and constraint satisfaction algorithms.
Computational Feasibility:
- Due to its small size, the 4×4 Queens Problem is computationally feasible to solve exhaustively without excessive computational resources, allowing for the identification of all possible solutions.
Educational Significance:
- The 4×4 Queens Problem serves as a valuable educational tool for introducing beginners to algorithmic problem-solving, recursion, backtracking, and combinatorial search algorithms.
Variants:
- Variants of the 4×4 Queens Problem may involve finding all distinct solutions, counting the total number of possible configurations, or extending the problem to larger board sizes.
Algorithmic Application:
- By solving the 4×4 Queens Problem, learners can understand fundamental algorithmic techniques such as backtracking, graph coloring, and constraint satisfaction, paving the way for tackling larger instances of the N-Queens Problem.
Insights and Patterns:
- Exploring the 4×4 Queens Problem provides insights into the symmetries, constraints, and patterns inherent in the arrangement of queens on a chessboard, facilitating the development of strategies for larger instances.
b) Write a note on travelling sales man problem.

Path
a –> b –> c –> c –> a
a –> b –> c –> d –> a
a –> c –> d –> b –> a
a –> c –> b –> d –> a
a –> d –> c –> b –> a
a –> d –> b –> c –> a
Sum
3 + 4 + 2 + 6 = 15
3 + 9 + 2 + 8 = 22
6 + 4 + 2 + 8 = 15
6 + 9 + 4 + 8 = 27
8 + 2 + 9 + 3 = 22
8 + 4 + 9 + 6 = 27
Optimal minimum path is 15
The best optimal paths are:
a –> b –> d –> c –> a
a –> c –> d –> b –> a
The Traveling Salesman Problem (TSP)
The Traveling Salesman Problem (TSP) is a classic and well-known computational problem in the field of optimization and algorithmic graph theory. It is a combinational optimization problem that seeks to find the shortest possible route that visits a set of given cities and returns to the original city.
Key Aspects:
Objective:
- The goal of the TSP is to find the shortest possible route that visits each city exactly once and returns to the original city.
Combinatorial Nature:
- The TSP is classed as an NP-hard problem, meaning that it is computationally infeasible to solve for large inputs using current algorithmic approaches.
Applications:
- TSP has wide-ranging practical applications such as vehicle routing, logistical planning, microchip fabrication, DNA sequencing, and network optimization.
Complexity:
- The number of possible solutions for the TSP grows factorially with the number of cities, resulting in a complex search space for finding the optimal route.
Solution Approaches:
- Various solution approaches are employed to address the TSP, including exact algorithms (such as dynamic programming and branch and bound) and approximate algorithms (such as genetic algorithms, simulated annealing, and ant colony optimization).
Variants:
- Variants of the TSP include the asymmetric TSP, in which the time or cost of travel between two cities can differ in each direction, and the TSP with time windows, where each city must be visited within a specified time window.
Optimization:
- TSP optimization aims to minimize the total distance traveled, although variants exist to minimize other factors such as time or costs.
Significance:
- Despite its computational complexity, the TSP remains a widely studied problem due to its real-world relevance and its representation of a fundamental class of optimization problems.
12. Write a short notes on any two of the following.
a) Breadth First Search (BFS).
Breadth First Search (BFS)
Breadth First Search (BFS) is a fundamental graph traversal algorithm that explores a graph level by level. It starts at a chosen vertex and explores all of the neighbor vertices at the present level, then moves to the vertices at the next level.
Key Concepts:
- Traversal Strategy:
- BFS explores a graph level by level, starting from the root or initial vertex and expanding to neighboring nodes before moving to deeper levels.
- Queue Data Structure:
- The key data structure used in BFS is a queue, which stores the nodes to be visited in the order they are discovered.
- Visited Nodes:
- To prevent revisiting nodes and avoid cycles, a visited flag or data structure is maintained to mark nodes as visited.
- Applications:
- BFS is commonly used for finding the shortest path in unweighted graphs, maze solving, level-order tree traversal, network broadcasting, and connected component identification.
- Completeness and Optimality:
- BFS is complete in finding the shortest path in unweighted graphs and guarantees an optimal solution.
- Time Complexity:
- The time complexity of BFS is O(V + E), where V represents the number of vertices and E the number of edges in the graph.
- Memory Usage:
- BFS may consume more memory than DFS due to the need to store all nodes in a level before proceeding to the next level.
- Key Behavior:
- BFS expands nodes in a breadth-wise manner, exploring all nodes at the current level before moving to the next level.
b) Depth First Search (DFS).
Depth First Search (DFS)
Depth First Search (DFS) is a fundamental graph traversal algorithm that explores as far as possible along each branch before backtracking. It is commonly used in tree and graph traversal problems and is based on the idea of visiting vertices or nodes recursively.
Key Concepts:
Traversal Technique:
- DFS visits nodes in depth-first order by exploring as far as possible along each branch before backtracking. It goes deep into a tree/graph before visiting the siblings.
Stack or Recursion:
- DFS can be implemented using a stack, where nodes are pushed and popped as they are visited, or through recursive function calls that simulate the stack behavior.
Visited Nodes:
- To prevent visiting the same node multiple times and avoid cycles, a visited flag or data structure is maintained to mark nodes as visited.
Applications:
- Common applications of DFS include finding connected components in a graph, topological sorting, cycle detection, pathfinding, and solving puzzles like mazes.
Completeness and Optimality:
- DFS is not complete in finding the shortest path in unweighted graphs but may be optimal under specific conditions.
Time Complexity:
- The time complexity of DFS is O(V + E), where V represents the number of vertices and E represents the number of edges in the graph.
Stack Over Recursion:
- Using a stack for DFS can be more space-efficient than recursion for large graphs, as recursion might lead to stack overflow errors.
Backtracking:
- Although DFS is not an explicit backtracking algorithm, it involves a similar concept of backtracking when no further nodes can be visited
c) Backtracking.
Backtracking:
Backtracking is an algorithmic technique used to systematically search for a solution to a computational problem. It involves incrementally building candidates for a solution and abandoning a candidate if it is determined that the candidate cannot possibly be completed to a valid solution. This technique is widely used to solve problems such as the N-Queens problem, Sudoku, graph coloring, and the knapsack problem.
Key Concepts:
Incremental Approach:
- Backtracking is based on an incremental approach, where candidates are built one by one with a set of parameters associated with each candidate.
Exploration and Elimination:
- The algorithm explores each possible solution by incrementally building it, and if at any stage it determines that the current candidate cannot lead to a valid solution, it eliminates that candidate and explores other possibilities.
Recursion:
- The backtracking algorithm typically uses recursive function calls to explore different choices and handle the intersections of different solutions.
State Space Tree:
- Backtracking can be visualized as traversing through the state space tree, where each node represents a partial candidate solution and the edges represent increments to build the solution.
Conflict Resolution:
- Backtracking efficiently handles conflicts and invalid states by discarding the candidates that lead to dead-ends or conflicts, thereby backtracking to a previous valid configuration.
Optimization:
- Various pruning techniques can be applied to optimize the backtracking process and reduce unnecessary exploration of potential solutions.
Applications:
- Backtracking is widely used in finding solutions for constraint satisfaction problems, puzzles, and optimization problems.
d) N-queen problem.
N-Queens Problem
The N-Queens problem is a classic chess puzzle where the goal is to place N chess queens on an N×N chessboard in a way that no two queens threaten each other. This means that no two queens share the same row, column, or diagonal.
Solution Approach:
Backtracking Algorithm:
- Typically, the N-Queens problem is solved using a backtracking algorithm.
- The algorithm systematically tries different combinations of queen placements, backtracking when it encounters conflicts.
Recursive Steps:
- The recursive steps involve trying to place a queen in each row while checking for row, column, and diagonal conflicts.
- If a valid configuration is found, the process continues to place queens in the next row. If not, backtracking occurs.
Constraints:
- The main constraint is to ensure that no two queens attack each other, meaning each queen is not in the same row, column, or diagonal as any other queen.
Optimizations:
- Several optimizations can be implemented, like pruning branches that would lead to conflicts early in the process.
Complexity:
- The time complexity of the N-Queens problem is O(N!), where N represents the number of queens to be placed. This complexity makes exhaustive search inefficient for large N.
Applications:
- The N-Queens problem has practical applications in combinatorial design, scheduling, and optimization.
Variants:
- Variants of the N-Queens problem include finding all possible solutions, not just one solution.
